Sistema de Geração de Malhas 3D Anti-Retenção Baseadas em Projeção Z-Depth¶
Cicero Moraes 3D Designer, Arc-Team Brazil, Sinop-MT
Rodrigo Dornelles Cirurgião Plástico, Núcleo de Plástica Avançada - NPA, São Paulo-SP
Everton da Rosa Cirurgião BMF, Hospital de Base, Brasília-DF
DOI |
Há uma grande demanda nas ciências da saúde para a geração de guias e splints baseados em superfícies não retentivas. Apesar de se tratar de um conceito relativamente simples, aplicá-lo em modelos orgânicos pode ser uma tarefa bastante desafiadora em face da complexidade das malhas geradas a partir tomografias e digitalizações por laser ou luz estruturada. O presente trabalho apresenta uma solução baseada na projeção de malhas por z-depth, que simplifica o processo mas não compromete a precisão dos modelos. Graças a flexibilidade do Python script foi possível portar a solução para o add-on OrtogOnBlender permitindo ao usuário não recorrer a programas externos, tornando o processo mais produtivo.
Importante
Este material utiliza a seguinte licença Creative Commons: Atribuição 4.0 Internacional (CC BY 4.0).
Como Funciona a Projeção por Z-Depth¶
Grosso modo, o Z-depth é uma imagem com dados de profundidade de uma cena 3D. Quanto mais claro um pixel, mais próximo do observador ele está, quando mais escuro, mais distante.
Nos softwares de computação gráfica o z-depth pode ter inúmeras utilidades, desde parâmetro para foco/desfoco de uma imagem até a projeção de vértices para mapeamento ou modelagem, justamente o que será abordado neste capítulo.
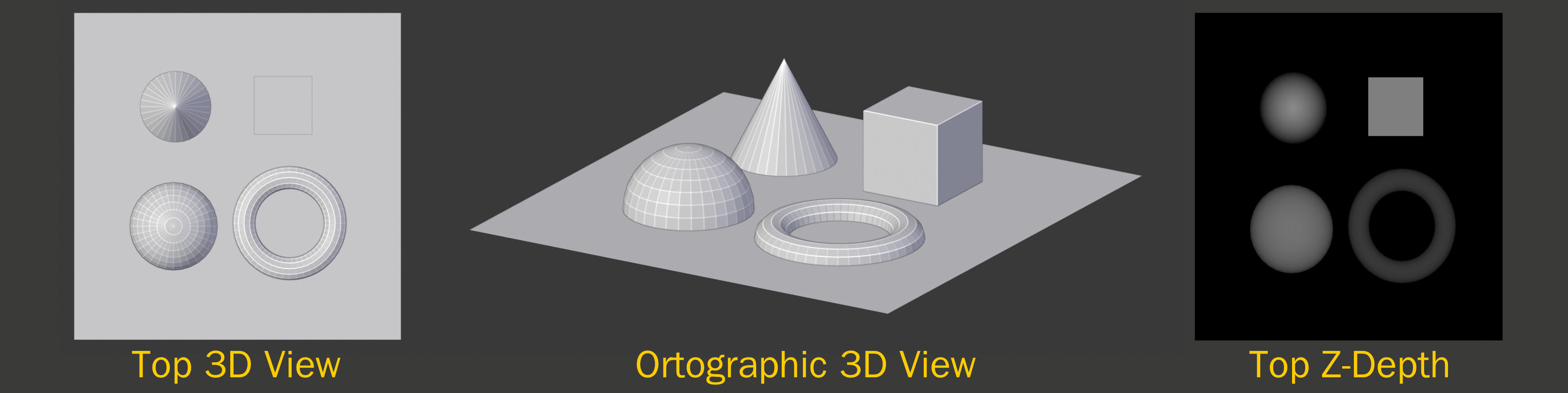
Exemplo de uma imagem z-depth criada a partir de uma cena 3D.¶
Na ilustração de exemplo (Figura 1) temos uma cena em 3D composta por vários elementos posicionados sobre um plano. O ponto de visualização utilizado como parâmetro de criação da projeção z-depth foi uma vista em topo (Top 3D View). Ao observarmos a cena de uma altura diferente (Ortographic 3D View) vemos que a parte mais baixa da cena é o plano e que as partes mais altas são a ponta do cone e a parte superior da caixa. A imagem z-depth criada reflete essas características, a parte mais escura é o plano, que fica mais distante do observador e as mais próximas são a ponta do cone e o topo da caixa.
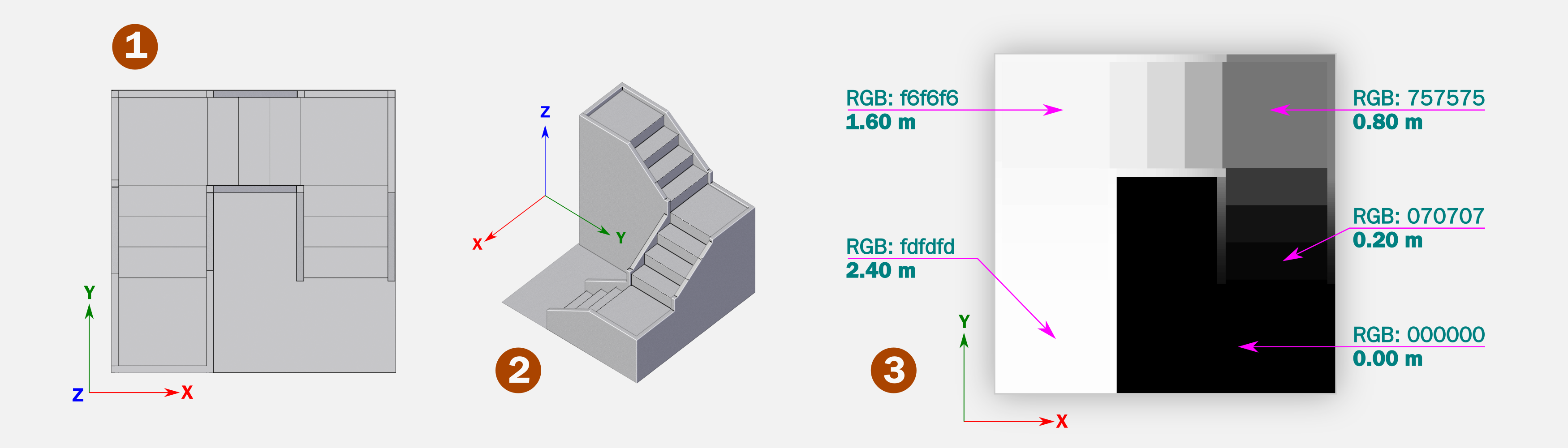
Escadaria convertida em uma imagem z-depth.¶
Neste outro exemplo (Figura 2) temos uma escadaria também visualizada pelo topo (1). Trata-de de uma imagem ortográfica e como tal, um dos eixos perde as informações, no caso o eixo Z ainda está lá, mas só vemos dados dos eixos X e Y. Se observarmos pela diagonal em uma altura diferente poderemos ver todos os eixos e termos uma ideia mais volumétrica do modelo (2). A imagem z-depth gerada (3) é uma matriz bidimensional como toda imagem e nesse caso conta apenas com os eixos X e Y. O truque mora na intensidade das cores (escala de cinza), esses dados funcionam como o eixo Z! Simplificando bastante para viabilizar a explanação, temos o piso que é representado pela cor preta ou 000000 no padrão hexadecimal do RGB. O valor zero também corresponde a altura 0.00 m. O primeiro degrau é um pouco mais claro, com o RGB em 070707 o que corresponde a altura de 0.20 m. E assim segue até o último degrau com o RGB de fdfdfd e a altura de 2.40 m. O valor máximo do RGB, segundo o padrão hexadecimal é de ffffff, isso significa que o ponto de observação de topo está um pouco mais alto que o último degrau. Por conta disso é importante estabelecer uma referência de altura para que as projeções dos objetos no z-depth sejam compatíveis com a cena original.
Essa explicação evidencia que, se podemos converter um objeto 3D em uma imagem z-depth, também podemos reconstruir essa imagem em um objeto 3D!
Reconstruindo o Z-Depth em 3D¶

Cena original e reconstruída a partir de uma imagem z-depth.¶
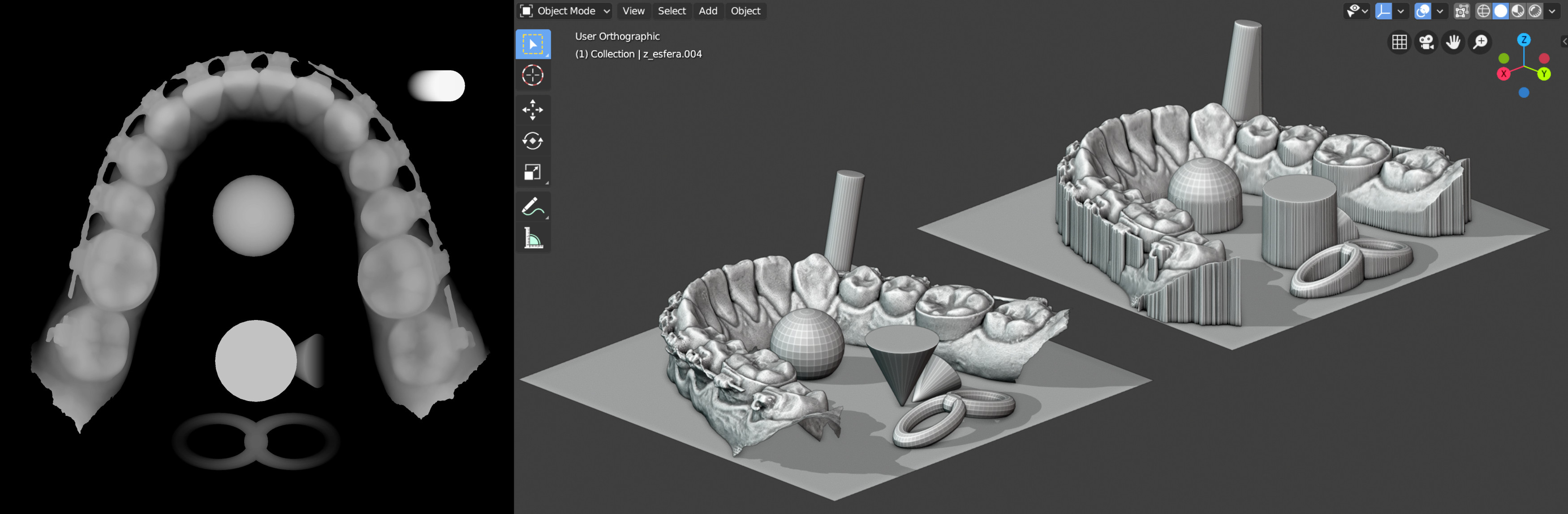
Seguindo o exemplo das cenas anteriores temos uma ilustração (Figura 3) com a cena observada pela câmera de referência para a projeção do z-depth (Top 3D View), a cena visualizada de outro ângulo (Ortographic 3D View), a imagem resultante da projeção (Top Z-Depth) e a reconstrução feita a partir da imagem (Z-Depth Reconstruction).
Pode parecer que houve algum problema na reconstrução, posto que as esferas não estão completas e na projeção inferior das mesmas temos três buracos, mas está correto. Sabemos que há um piso sem buracos e que se tratam de esferas completas porque visualizamos a cena de outro ponto de vista (Ortographic 3D View), capturando assim mais informações acerca da mesma. A imagem usada para a reconstrução não contém dados das regiões ocultas ao observador, sendo assim, foi reconstruído apenas o que estava disponível na projeção.
Essa aparente limitação é na verdade essencial para a criação de superfície não-retentivas, posto que são justamente as parte ocultas a partir de um ponto de vista as responsáveis pela retenção dos objetos.
O Problema das Superfícies Retentivas¶
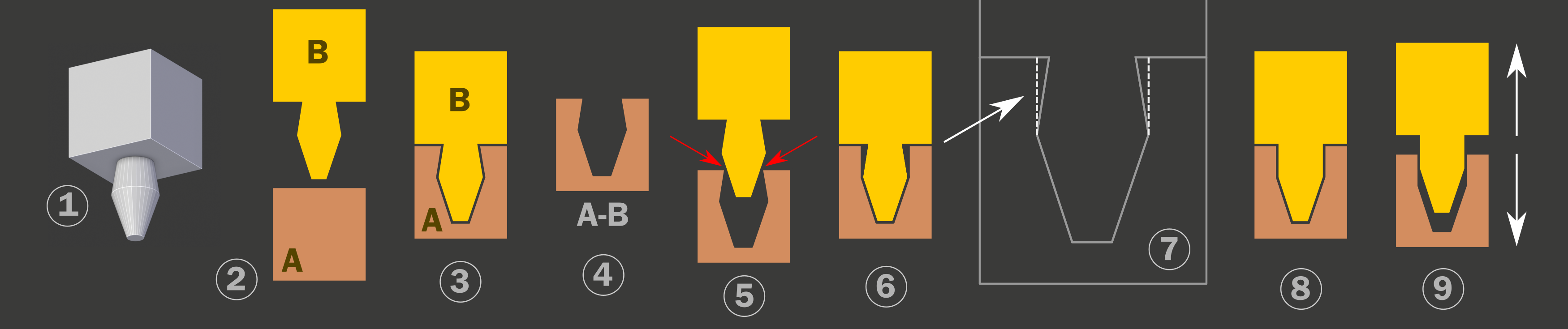
Problema de retenção e solução do mesmo.¶
Para entendermos o problema da retenção, tomemos como exemplo um objeto que será usado como base para a criação de um ecaixe (Figura 4, 1). Esse elemento será encaixado em um cubo de igual dimensão da parte superior, aqui representado pelo elemento A, sendo o B o elemento base apresentado em corte (2). No OrtogOnBlender a maioria dos usuários busca mover os elementos até a sua posição final, criando uma região de intersecção dos mesmos (3). Em seguida é efetuado um cálculo booleano de subtração de malhas A-B, resultando em um objeto com um buraco nas mesas dimensões da ponta da nossa base (4). O problema mora justamente no momento de encaixar os dois elementos. Isso acontece porque o meio da parte inferior é mais grosso que a base, assim o objeto vai até uma parte e não entra mais (5). Para que ele entrasse sem retenção, seria necessário projetar a parte maior da ponta até a base final da parte superior (6 e 7). Isso alteraria a forma do modelo em relação ao original, não contendo as reentrância daquele (8) e permitindo uma movimentação livre de encaixe depois do cálculo booleano (9).
Como Criar Modelos Anti-Retenção no OrtogOnBlender¶

Seção da criação da superfície anti-retenção no OthersOnBlender.¶
Como se trata de uma ferramenta experimental os botões se encontrarão na aba Other, correspondente ao OthersOnBlender (Figura 5), submódulo do add-on OrtogOnBlender [MdRD20a].

Cubo com a região de projeção da superfície não-retentiva.¶
Para definir qual região será utilizada para gerar a superfície não-retentiva é necessário clicar no botão “Import Base Box” (Figura 6). Assim que o o fizer aparecerá um cubo na cena com a escrita “TOP” na parte superior, indicando o ponto de vista no qual será gerado o z-depth. Ao importar o cubo o botão clicado anteriormente ficará desabilitado para evitar qualquer confusão com cubo duplo no momento de criar a projeção.
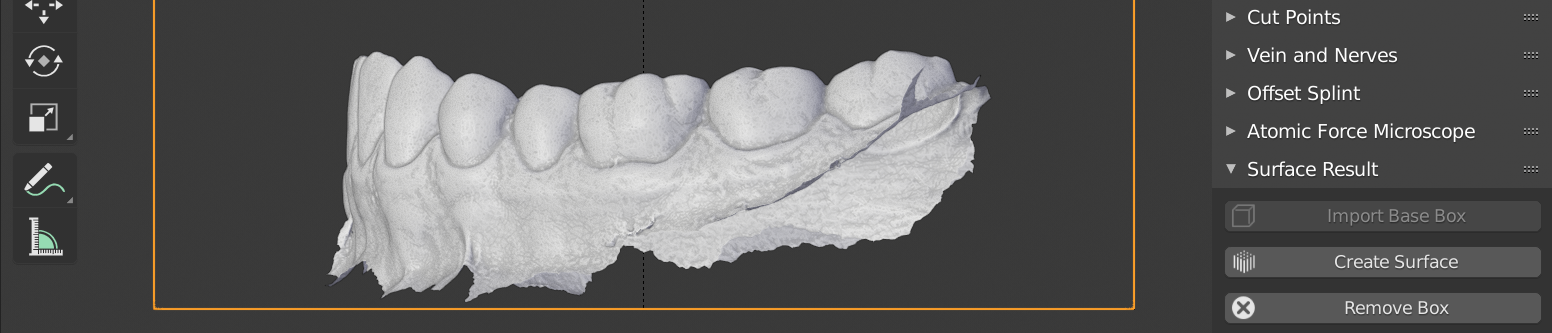
Ajuste da posição da Base Box.¶
O usuário pode então ajustar a posição do cubo até se adequar a região que pretende capturar (Figura 7).

Criação da malha retentiva.¶
Assim que o cubo é posicionado, basta clicar em “Create Surface” e aguardar alguns segundos para que a malha seja gerada (Figura 8).
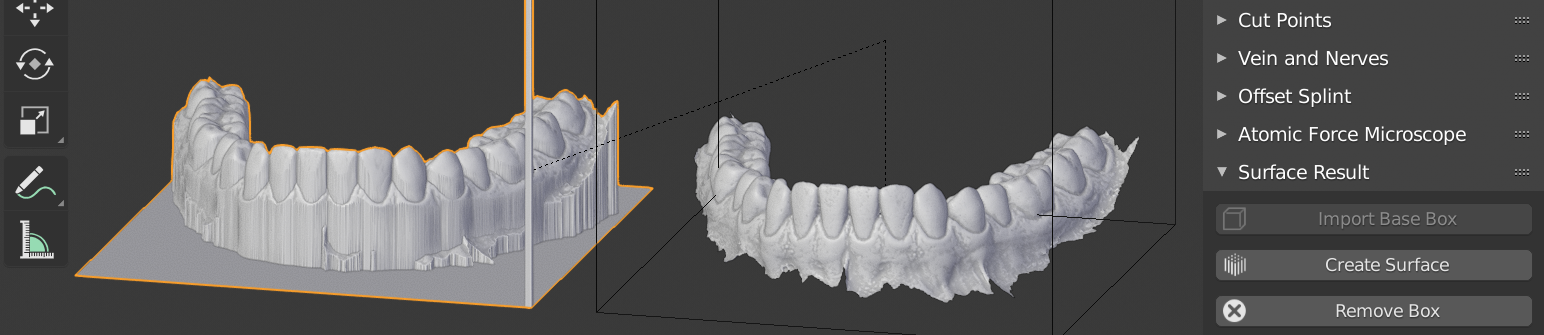
Criação da malha não-retentiva.¶
A superfície criada pode ser deslocada caso o usuário assim o deseje (Figura 9). Neste caso os modelos foram posicionados lado-a-lado para que possamos compará-los. Em um primeiro momento o comando lembra muito uma extrusão, mas é diferente da mesma, posto que o que faz é apenas fechar os espaços que não são contemplados pelo z-depth. Como a projeção foi feita pela parte superior (TOP) o comando simplesmente fechou as laterais evitando as áreas faltantes as quais foram abordadas na parte inicial deste capítulo onde apareceram meias esferas e buracos no plano.
O modelo gerado cria dois elementos que não estão presentes no original: uma base informando o limite do cubo de referência e uma haste correspondente a distância de controle do z-depth. O cubo de referência tem as dimensões de 80x80x80 mm, o suficiente para capturar uma arcada completa ou partes de uma face onde se deseja projetar uma superfície não-retentiva.
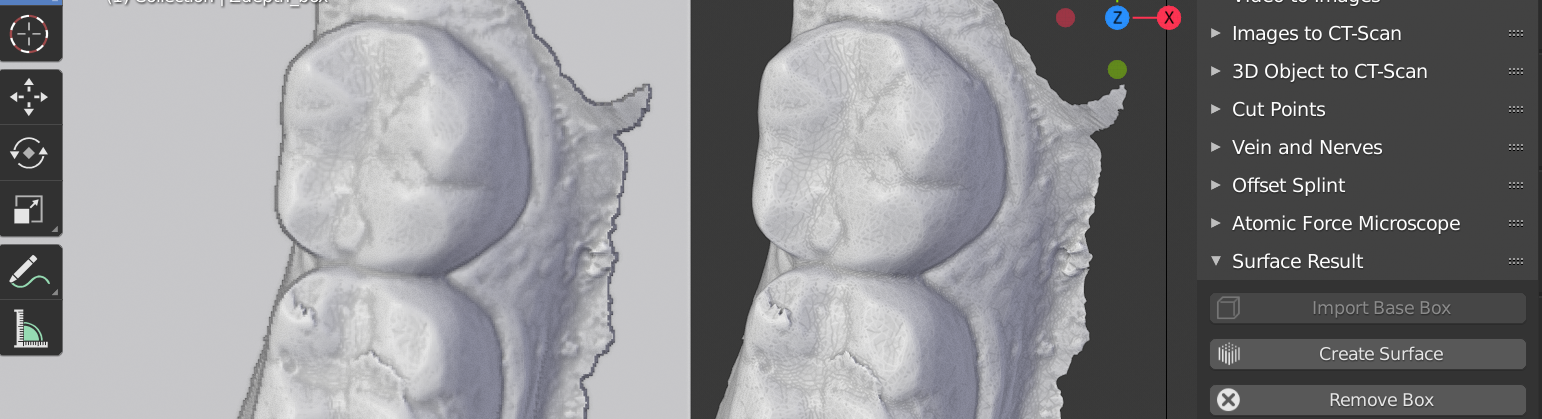
Modelos observados pelo topo.¶
Ao observarmos os modelos pelo ponto de vista utilizado para gerar o z-depth, só conseguirmos diferenciá-los pela base que a malha à esquerda possui, ou seja, trata-se da superfície não-retentiva (Figura 10). Isso acontece porque essa vista contém todos os dados capturados pelo z-depth.
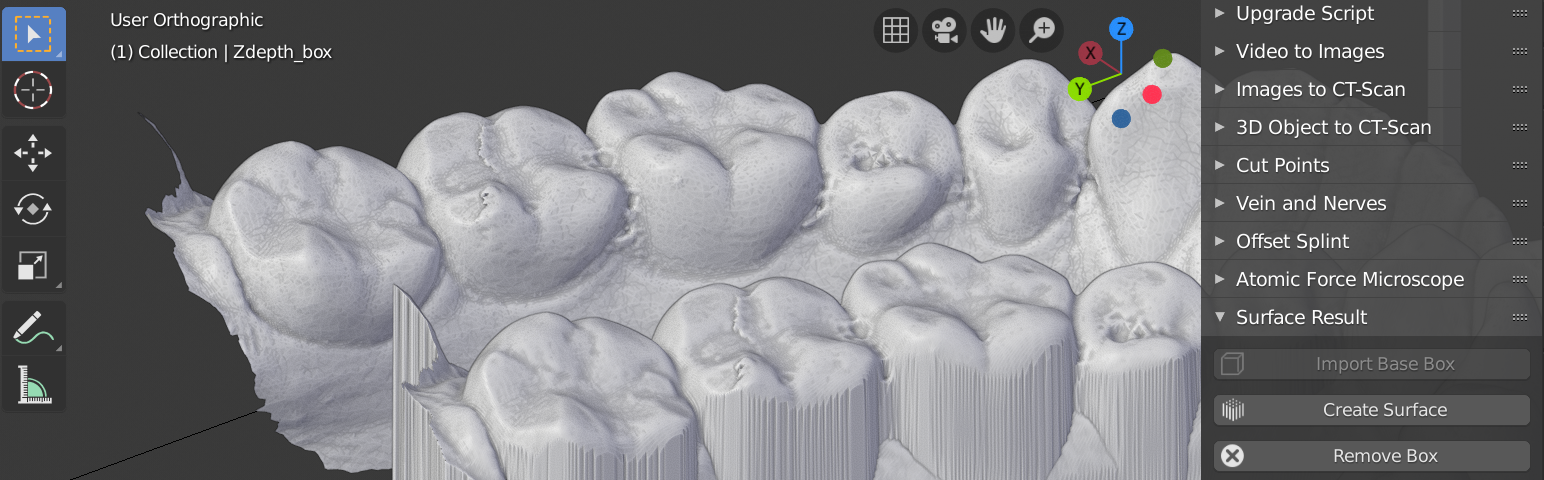
Modelos observados pela lateral.¶
As diferenças ficam mais evidenciadas quando os modelos são observados pela lateral, onde as reentrâncias inferiores dos dentes dão lugar a uma superfície lisa e não-retentiva, o que facilitará o encaixe, por exemplo, de um guia (Figura 11).
Testando os Modelos Antes da Impressão 3D¶
A cada dia cresce o número de usuários do OrtogOnBlender que adquirem impressoras 3D e fazem uso dessa tecnologia para a criação de guias cirúrgicos. Por se tratar de uma tecnologia com custo relativamente alto e também com tempo de impressão lento, é imprescindível que o modelo a ser impresso não contenha falhas, tanto estruturais no sentido da malha, como na funcionalidade do objeto.
Uma forma de entender o funcionamento e vantagem da superfície de não-retenção é justamente testando o encaixe com ferramentas de simulação de colisão oferecidas pelo OrtogOnBlender [MdRD20b]. As ferramentas podem ser usadas para testar o encaixe de arcadas, encaixe de splints e de guias de modo tornar o processo mais assertivo e barato, já que dispensará impressões de testes.

Malhas criadas com boolean na parte superior e rotacionadas para melhor visualização.¶
Foram criadas duas malhas a partir de um cálculo booleano de subtração para sulcar a região de intersecção dos dentes (Figura 12). As mesmas foram posicionadas acima das arcadas para que a simulação física fosse efetuada.
Aviso
Para compreender melhor o teste é necessário assistir o vídeo que está disponível neste link: https://youtu.be/45T1I57xPF0
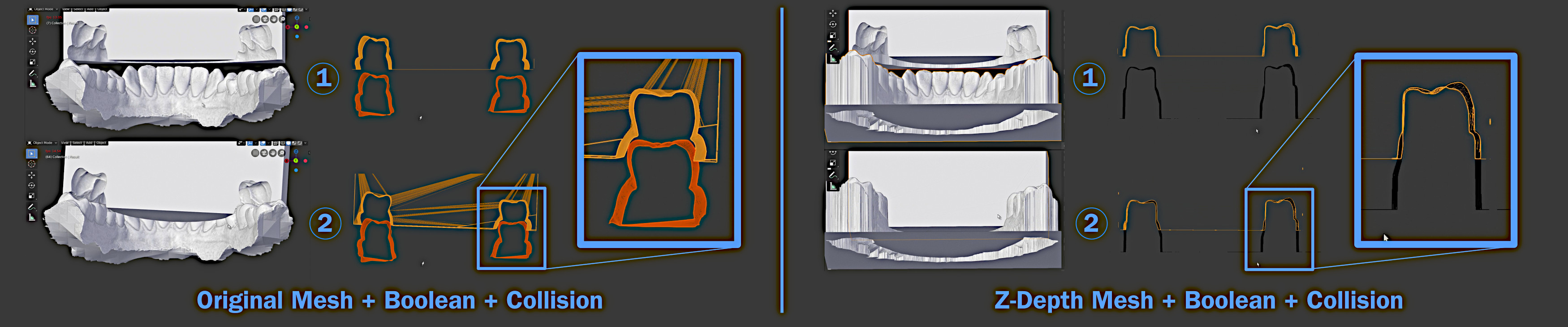
Comparação no encaixe da malha original e da malha reconstruída a partir do z-depth.¶
Ao proceder com a colisão (Figura 13) a malha original tocou regiões com retenção e isso desestabilizou a malha que deveria se encaixar fazendo com que a mesma ficasse inclinada (à esquerda). Isso evidenciou o problema de se utilizar o boolean com a malha original sem o tratamento de encaixe. Já a malha que foi reconstruída pela imagem z-depth se encaixou com perfeição (à direita).

A mesma cena com projeções diferentes do z-depth.¶
Além das facilidades supracitadas, o usuário pode criar a projeção do z-depth a partir de qualquer rotação que desejar, lembrando que a projeção é feita a partir do topo (Figura 14).
Essa abordagem pode ser muito útil quando o cirurgião, por exemplo, tem um espaço de posicionamento de guia muito limitado, forçando-o a inserir a estrutura a partir de um ângulo definido.
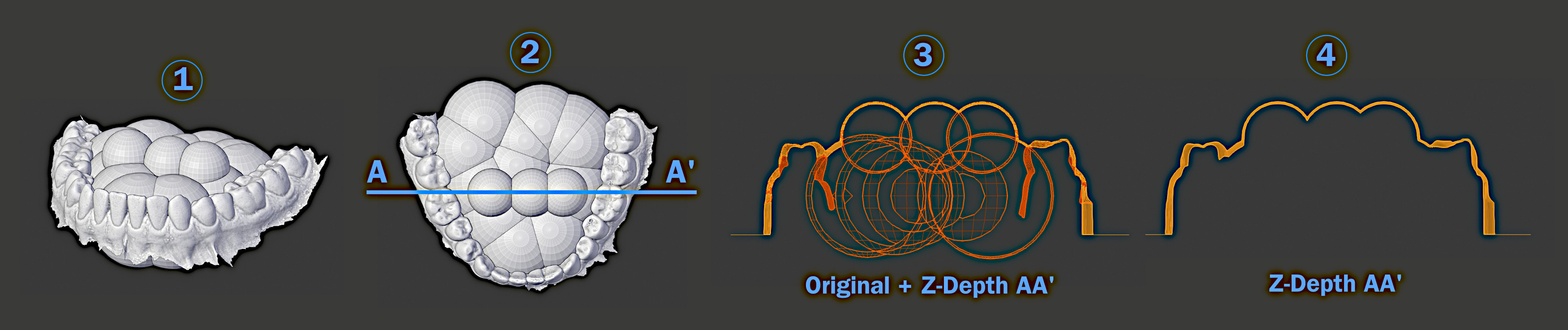
Malha limpa resultante de um emaranhado de meshes sobrepostas.¶
Uma outra vantagem deste sistema é a possibilidade de gerar malhas limpas a partir de um agrupamento de meshes. Podemos tomar como exemplo a arcada utilizada neste capítulo, inserindo uma série de esferas na região interna da mesma (Figura 15, 1). Para entender a complexidade da estrutura é necessário fazer um corte ou um clipping (2) de modo a ver a série de intersecções que acontecem no interior (3) e como a malha resultante é limpa (4) quando comparada com o emaranhado orginal. Ou seja, o usuário pode fazer a projeção mesmo se tratando de um grupo de objetos distindos, o resultado será uma malha única, limpa e sem retenção.
Dica
Para melhorar o encaixe da malha o usuário pode criar uma cópia do objeto a ser projetado e fazer um redimensionamento por normal (Alt+s) com o valor de 0,05. O cálculo booleano será feito com essa malha mais grossa, garantindo assim o sucesso do encaixe posterior.
Conclusão¶
A ferramenta de geração de malhas não-retentivas mostrou-se funcional e flexível ao criar malhas limpas, próprias para cálculos booleanos, permitindo ao usuário gerar modelos de splints, guias e demais formas para encaixe, podendo escolher o ângulo que esse elemento vai se adaptar a superfície de conformação, seja ela uma arcada dentária, um osso, um remanescente de tecido mole ou uma estrutura sólida qualquer.
- MdRD20a
Cicero Moraes, Everton da Rosa, and Rodrigo Dornelles. Ortogonblender - documentação oficial. 2020. URL: http://www.ciceromoraes.com.br/doc/pt_br/OrtogOnBlender/index.html.
- MdRD20b
Cicero Moraes, Everton da Rosa, and Rodrigo Dornelles. Ortogonblender - simulação de colisão física. 2020. URL: http://www.ciceromoraes.com.br/doc/pt_br/OrtogOnBlender/OrtogOnBlender_Como_Funciona.html#mandible-collision.